Do kites and celestial mechanics have anything in common?
- Emese Kővári
- Jul 24, 2016
- 3 min read
Astronomy has always been one of the elds of science that showed the most dynamical development. However, the progress that took place in the last few years is almost incredible. We performed a successful landing on the core of a comet, found the long-awaited Higgs boson particle, discovered gravitational waves and hence were provided with a completely new view of the Universe. The increasing number of Earth-like planets in habitable zones even raises the question if we are alone or not. But the list is endless... Citing the subtitle of one of the lectures at ESOF, 'we are cracking the mysteries of physics'. And as for mysteries, my aim is to present the next one, i.e. a riddle in celestial mechanics being solved just a few months ago by two researchers at Eötvös Loránd University. Celestial mechanics as one of the branches of astronomy deals with the motions and dynamics of celestial bodies. The n-body problem as a main issue of it concerns the problem of n point-like bodies moving under the mutual Newtonian gravitational forces. The case n = 2 (two-body problem) was solved by Newton himself, back in the 17th century. However, no general solution exists for values n greater than 3, highlighting the complexity of the problem and at the same time forcing us to focus on an important subtype, the so-called central con gurations. A con guration is called central if the resulting forces on each body are directed towards the center of mass of the system or to put it another way, if the formation or pattern given by the bodies of the system (e.g. a triangle in the case of 3 bodies or a tetrahedron in the case of 4), does not change during the motions. The solution of the central three-body problem still dates back to the 18th century, to Lagrange and Euler. However, analitical results for n > 3 have been unknown until now, when some 200 years after the work of the greatist mathematicians of the 18th century, Bálint Érdi professor emeritus and Zalán Czirják PhD student achieved a major breakthrough in celestial mechanics by deriving a complete analitical solution for the axisymmetric case of planar central con gurations of four bodies.
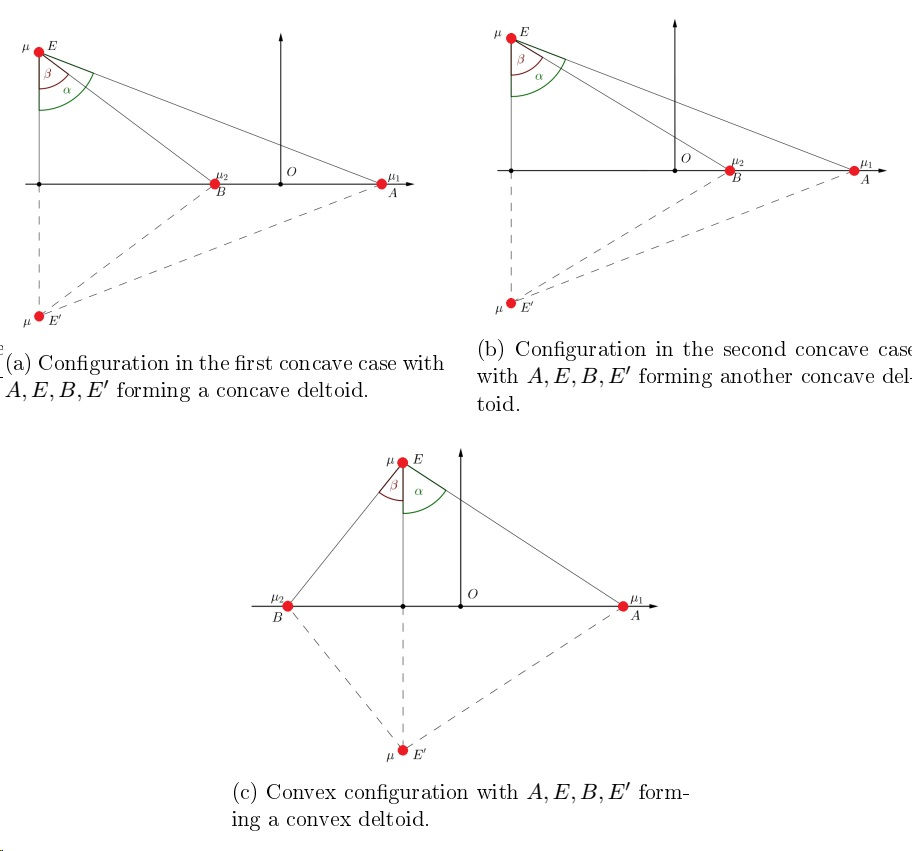
Figure 1: Possible con gurations of four bodies (e.g. planets or stars) with an axis of symmetry going through two bodies (A and B) and two other bodies of equal mass (E and E0) situated symmetrically with respect to this axis. The corresponding masses are labeled with µ1; µ2; µ; µ, respectively. O is the center of mass of the system.
As shown in Fig. 1 the possible central con gurations correspond to a convex and two concave deltoids. These are often called kite con gurations due to the similarity in shape. The symmetry is based on the fact that two of the four bodies (labeled with E and E0) are situated symmetrically with respect to the axis of symmetry and have equal masses as well. Investigating the equations of motion of this system we face a seemingly insoluble problem. But two admirable ideas led the scientists to a solution: rstly, they introduced angle coordinates (see α and β in Fig. 1) instead of Descartes coordinates, As shown in Fig. 1 the possible central con gurations correspond to a convex andtwo concave deltoids. These are often called kite con gurations due to the similarity inshape. The symmetry is based on the fact that two of the four bodies (labeled with Eand E0) are situated symmetrically with respect to the axis of symmetry and have equalmasses as well. Investigating the equations of motion of this system we face a seeminglyinsoluble problem. But two admirable ideas led the scientists to a solution: rstly, theyintroduced angle coordinates (see α and β in Fig. 1) instead of Descartes coordinates























Comments